Základní funkce

Obecně o funkcích

V předchozím textu byly ukázány jednoduché výpočty (jako bylo sčítání, odčítání, …) nad hodnotami uloženými v buňkách. Tabulkové procesory ale disponují celou řadou dalších pokročilých možností, jak početně zpracovávat data uložená v buňkách. Tyto možnosti poskytují tzv. funkce, díky kterým je možné provádět velmi jednoduše i poměrně komplikované výpočty, a to dokonce bez konkrétní znalosti potřebných vzorců.

Pro každou funkci je charakteristické, že má určitý název a volitelně i několik vstupních parametrů, nad kterými provede výpočet a vrátí do příslušné buňky výsledek. Pro funkce je typické, že se zadávají ve formě NÁZEV_FUNKCE(x1; x2; …; xn), kde x1, x2, …, xn představují jednotlivé parametry. Na Obr. 16 v bodu 1 je ukázán způsob zápisu funkce pro sečtení dvou (či více čísel). Název funkce je SUMA a v kulatých závorkách jsou uvedeny odkazy do buněk C3 a D3 oddělené středníkem (tato funkce umožňuje tímto způsobem zadat prakticky libovolné množství odkazů či čísel). Jednotlivé odkazy představují zmíněné vstupní parametry. V části 2 je pak vidět výsledek výpočtu.

Za jednoduchou funkci by bylo možné považovat např. i dříve uvedené sčítání dvou hodnot. Parametry jsou v takovém případě odkazy na buňky s hodnotami (nebo přímo hodnoty) a „názvem“ je operátor +. Z hlediska zadávání se nejedná o klasickou funkci, jako je tomu u funkce SUMA, která počítá prakticky totéž. Protože součet (rozdíl, násobení, dělení, …) představuje často používanou operaci, je umožněn i tento zjednodušený zápis.

Stejně jako u jednoduchých výpočtů ani v případě zadávání funkcí není nutné zapisovat adresy buněk ručně, ale během psaní vzorců je možné využít přímého pokliku myší do požadovaných buněk. Také relativnost (resp. absolutnost) jednotlivých odkazů se chová stejným způsobem, jaký byl popsán v úvodní kapitole, o čemž je možné se přesvědčit rozkopírováním vzorce z Obr. 16 do dalších buněk. Automatickou aktualizaci relativních odkazů ilustruje Obr. 17.

Základní statické funkce

Většina tabulkových procesorů disponuje velkým množstvím vestavěných funkcí, které je možné využívat. Názvy jednotlivých funkcí se mohou v různých tabulkových procesorech lišit (některé používají například názvy přeložené do češtiny, jiné vycházejí z anglických názvů).

Protože není v lidských silách si zapamatovat všechny funkce, obsahuje každý tabulkový procesor dialog, který výběr požadované funkce usnadňuje jejich rozčleněním do logických skupin. Např. v programu Excel lze tento dialog vyvolat kliknutím na ikonku s písmeny fx, umístěnou těsně před řádkem vzorců (Obr. 18).

Dialog Vložit funkci (Obr. 19) se ovládá velmi intuitivně, v rozbalovacím seznamu stačí vybrat skupinu požadovaných funkcí (viz část 1) a poté v seznamu zobrazených funkcí vybrat požadovanou. Při výběru lze využít i stručného popisu, který se pro každou funkci zobrazí pod seznamem (viz část 2).

Přestože se pomocí tohoto dialogu dají potřebné funkce dohledat poměrně efektivně, je u nejčastěji používaných funkcí užitečné si je pamatovat.

Určení minima a maxima

Pro určení minimální hodnoty je možné použít funkci nazvanou MIN. Tato funkce má proměnlivý počet parametrů, tzn., že může určit minimální hodnotu z různého počtu čísel. Lze jí použít na pevný výčet hodnot, jak je znázorněno na Obr. 20.

Pokud by se hodnoty v průběhu vyhodnocování mohly měnit, je výhodnější jednotlivé hodnoty psát do samostatných buněk a ve funkci použít odkazy na tyto buňky (Obr. 21).

Přístup znázorněný na Obr. 21 je výhodný s ohledem na možnou změnu vyhodnocovaných čísel, kterou je možné provést snadnou změnou některé z odkazovaných buněk. Pokud by bylo množství vyhodnocovaných buněk větší, bylo by výhodnější se místo na jednotlivé buňky odkázat na blok buněk (viz kapitola Blok buněk), jak znázorňuje Obr. 22.

Přestože se postup na Obr. 22 nemusí zdát jako příliš výhodný (v porovnání s Obr. 21), u většího počtu dat je úspora času a práce zřejmá.

Pro určení maximální hodnoty je možné použít funkci MAX, která se chová stejně, jako právě popsaná funkce MIN. Ilustrace této funkce je uvedena na Obr. 23.

Jednotlivé funkce je možné ve výpočetním výrazu kombinovat. Obě popsané funkce by bylo možné použít pro určení rozsahu (rozdílu mezi maximální a minimální hodnotou) hodnot. Způsob zkombinování obou funkcí je znázorněn na Obr. 24.

Na Obr. 24 byly pro názornost minimální a maximální hodnoty vypočteny zvlášť. Dále byly obě funkce použity v rámci jednoho výrazu. Jejich propojení umožnil operátor mínus (v podstatě se tedy jedná o kombinaci tří funkcí).

Program postupuje tak, že vypočítá hodnotu obou funkcí (12 a 1) a těmito hodnotami zamění obě funkce (z matematického hlediska by se dalo hovořit o substituci). Výsledkem je zjednodušený výraz =12-1, který již program snadno spočítá. Že je výsledek správný, je patrné na první pohled díky zvlášť vypočítaným hodnotám minima a maxima (Rozsah by pochopitelně bylo možné vypočítat i s využitím těchto dílčích hodnot, ale použitím obou funkcí v jednom výrazu je možné ušetřit místo v tabulce).

Za povšimnutí na Obr. 24 stojí také fakt, že označená oblast nemusela být zcela vyplněna hodnotami. V pravém dolním rohu je nevyplněná buňka, kterou program při výpočtu ignoroval. Pokud by ale došlo k dodatečnému doplnění některé hodnoty na tuto pozici, byla by zahrnuta do automatického přepočtu.

Výpočet součtu a průměru

Výpočet součtu pomocí funkce SUMA byl již zmíněn v kapitole Obecně o funkcích, ve které byla pro jednoduchost prezentována možnost sečtení malého počtu čísel. Stejně jako ve funkcích pro určení minimální a maximální hodnoty je také u funkce SUMA možné jako vstupní parametr zadat nejen výčet hodnot, ale také oblast buněk, jak ilustruje Obr. 25.

Funkce, které pracují s oblastí hodnot, jako jsou např. funkce SUMA, MIN nebo MAX, mohou jako vstupní parametr přebrat i více oblastí zároveň. V takovém případě je třeba jednotlivé oblasti oddělit středníkem, jak je znázorněno na Obr. 26.

V případě Obr. 26 by bylo možné dílčí oblasti označit jako jednu velkou s tím, že prázdné hodnoty budou ignorovány, ale může nastat situace, kdy se sčítané oblasti budou vyskytovat na různých místech a jejich souhrnné označení by již nebylo možné.

Aritmetický průměr je definován vztahem:

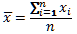
Ze vzorce je patrné, že by bylo možné vypočítat aritmetický průměr jako podíl výsledků funkce SUMA a zatím nedemonstrované funkce POČET, která vrací počet čísel v určité oblasti. Většina tabulkových procesorů ale pro výpočet poskytuje samostatnou funkci, v případě programu Excel se jedná o funkci PRŮMĚR, která se snáze zadává a která se chová obdobným způsobem, jako všechny doposud představené funkce.

Funkce PRŮMĚR je předvedena na Obr. 27.

V kapitole Určení minima a maxima byla zmíněna možnost kombinovat více funkcí v rámci jednoho výrazu. Byl popsán výpočet rozdílu mezi výsledky dvou funkcí. Funkce je možné kombinovat i jiným způsobem. Pokud je výsledkem jedné funkce číslo a druhá funkce má jako vstupní parametr obecně nějaké číslo, je možné místo parametru druhé funkce vložit první funkci (obdobně, jako lze použít odkaz na buňku či oblast buněk).

V situaci, kdy existuje několik souborů dat, ze kterých je zapotřebí vypočítat dílčí součty a tyto součty poté zprůměrovat, lze postupovat různými způsoby. Obr. 28 znázorňuje postup, ve kterém se nejprve vypočítají součty dat v jednotlivých sloupcích (funkce SUMA odkazující se na příslušný sloupec dat), a teprve z těchto dat je následně vypočítán průměr (funkce PRŮMĚR odkazující se na buňky s vypočítanými součty).

Pokud by součty byly pro potřeby vyhodnocování nedůležité (jednalo by se pouze o mezivýsledek), je možné zadat výpočet tak, že funkci PRŮMĚR se předají jednotlivé funkce SUMA jako vstupní parametry (oddělené středníkem), jak znázorňuje Obr. 29.

Jak je patrné z pravých částí Obr. 28 a Obr. 29, výsledek je v obou případech totožný.

Výpočet směrodatné odchylky

Směrodatná odchylka popisuje, jak se jednotlivé naměřené hodnoty liší od průměrné hodnoty. Při výpočtu směrodatné odchylky záleží na tom, zda naměřené hodnoty představují pouze výběrové hodnoty (nejsou k dispozici všechny hodnoty, pouze jejich vzorek) nebo zda představují všechny hodnoty.

Na Obr. 30 jsou graficky znázorněny dvě desetičlenné skupiny čísel. Obě skupiny mají průměrnou hodnotu rovnou 11 (na obrázku znázorněna červenou tečkovanou čárou), přesto je na první pohled zřejmé, že je nelze pokládat za stejné.

V první skupině je směrodatná odchylka 1,211, v druhém případě je směrodatná odchylka 0,447. Ve druhé skupině je směrodatná odchylka menší a tedy jednotlivé hodnoty se nacházejí blíže průměru, než je tomu v první skupině (jsou méně rozptýleny). Průměrná hodnota ve druhé skupině tedy může být „blíže pravdě“ (skutečné hodnotě měřené veličiny) než ve skupině první, a to navzdory shodnému průměru.

V případě, že naměřené hodnoty představují vzorek hodnot, je směrodatná odchylka definovaná vztahem:

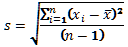
, kde n je počet hodnot.

V případě, že naměřená data představují všechny hodnoty, je směrodatná odchylka definovaná podobným vztahem:

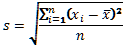
, kde n je opět počet hodnot.

Již z pohledu na vzorec je patrné, že pro výpočet směrodatné odchylky by bylo nutné při ručním výpočtu provést velký počet operací, přičemž přidání jedné hodnoty by znamenalo znovu provést všechny výpočty. Také riziko početní chyby je v tomto případě velké.

Většina moderních tabulkových procesorů má k dispozici již vestavěné funkce, které většinu potřebných výpočtů provedou automaticky. Takovými funkcemi jsou v případě programu Excel funkce SMODCH() a SMODCH.VÝBĚR().

Obě funkce mají proměnlivý počet parametrů, kterými jsou naměřené hodnoty. Tyto parametry je možné vyjmenovat a oddělit čárkami nebo zadat jako oblast dat, obdobně, jako tomu bylo i u předchozích funkcí.

Způsob výpočtu směrodatné odchylky ilustruje Obr. 31. Je z něj mimo jiné patrné, že směrodatná odchylka počítaná jako výběrová, se odlišuje od směrodatné odchylky populační. S rostoucím počtem dat se rozdíl mezi nimi zmenšuje.

Pomocí směrodatné odchylky (a průměru) je možné určit interval hodnot, ve kterém se s určitou pravděpodobností nachází skutečná hodnota měřené veličiny. Výsledek z Obr. 31 tak bylo možné interpretovat tak, že skutečná hodnota měřené veličiny se nachází

• v intervalu 10,6 ± 2,1 s pravděpodobností 99,74 % (hodnota 2,1 je trojnásobek výběrové směrodatné odchylky)
• v intervalu 10,6 ± 1,4 s pravděpodobností 95,44 % (hodnota 1,4 je dvojnásobek výběrové směrodatné odchylky)
• v intervalu 10,6 ± 0,7 s pravděpodobností 68,27 % (hodnota 0,7 je hodnota výběrové směrodatné odchylky)

Podmíněné výrazy

Užitečnými funkcemi jsou funkce, které umožňují vytvářet tzv. podmíněné výrazy. Podmíněný výraz lze slovně formulovat např. takto: „Pokud je hodnota X záporná, pak se mají sečíst čísla A a B. V opačném případě se má číslo A vynásobit dvěma.“ Je to tedy takový výraz, který vyhodnotí určitou podmínku („je X záporné?“), a pokud je podmínka platná („X je skutečně záporné“), provede se určitá operace („sečíst A a B“). Pokud je podmínka neplatná („X je kladné nebo nula“), provede se jiná operace („vynásobit A dvěma“).

Nejjednodušší funkcí pro tvorbu podmíněných výrazů je funkce KDYŽ(podmínka; výraz1; výraz2). Tato funkce má tři parametry. Prvním je vyhodnocovaná podmínka. Pro její vytvoření je možné použít odkazy na jiné buňky a standardní operátory pro porovnání (např. <, <=, =, =>, >). Druhým parametrem je výraz, který se má vypočítat v případě, že je podmínka pravdivá, a třetím parametrem výraz pro případ, že je podmínka nepravdivá.

Realizaci příkladu z prvního odstavce této kapitoly ilustruje Obr. 32. Za povšimnutí stojí fakt, že rovnítkem je uvozena pouze samotná funkce KDYŽ(), porovnávací a výpočetní výrazy uvnitř této funkce již rovnítkem nezačínají.

V jednotlivých parametrech funkce je možné použít i výstupy jiných funkcí. Lze tak sestavit podmínku, která bude vyhodnocovat maximální hodnotu z určité oblasti hodnost a na jejím základě pak vypočítá např. průměr z daných hodnot. Jak by použití dalších funkcí vypadalo v programu Excel, znázorňuje Obr. 33.

Na Obr. 33 je vidět, že v části podmínky je použita funkce MAX(). Pokud je výsledek této funkce v oblasti B3:C7 větší než 10, pak se má vypočítat průměr z hodnot v této oblasti. Tedy jako druhý parametr je použita funkce PRŮMĚR() s touto oblastí. Za povšimnutí stojí také konec podmíněného výrazu, který končí středníkem (který je oddělovačem parametrů ve funkcích) a za kterým již nic nenásleduje. To znamená, že v případě, že není podmínka funkce splněna, má zůstat příslušná buňka prázdná, resp. že její hodnota má být nula, jak je znázorněno na Obr. 34, kde byla maximální hodnota 11 změněna na hodnotu menší než 10.

Je zřejmé, že pokud je v rámci podmíněného výrazu možné využít jiných funkcí, pak je možné do podmíněného výrazu vložit i další podmíněný výraz. Pomocí vnořování podmíněných výrazů do sebe je možné vytvořit poměrně komplexní (a komplikovanou) logiku. Zároveň se ale s každým dalším vnořením výrazně zesložiťuje celý výraz (Proto nebudou vnořené výrazy blíže demonstrovány pomocí obrázků) a je snadné v něm udělat chybu.

Dalším méně známým způsobem, jak pracovat s podmíněnými výrazy, může být funkce SUMIF(). Tato funkce umožňuje provádět nad určitou oblastí součty těch hodnot, které odpovídají určité podmínce (např., že sčítat se mají pouze ty hodnoty, které jsou kladné).

Funkce SUMIF() má minimálně dva parametry. První z nich definuje oblast, nad kterou má být součet proveden, druhý definuje podmínku, kterou musí hodnoty v dané oblasti splnit, aby byly započteny do výsledného součtu. Použití této funkce ilustruje Obr. 35.

Na Obr. 35 je zobrazen prostý součet všech hodnot pomocí již dříve uvedené funkce SUMA() a podmíněný součet pomocí funkce SUMIF(). Prvním parametrem funkce SUMIF() byla oblast B4:C7, druhým parametrem byla podmínka >=0 definující pouze kladná čísla. Za povšimnutí stojí, že podmínka je uvedena v uvozovkách.

V případě dvouparametrové varianty funkce SUMIF() bylo vyhodnocení a sčítání provedeno nad stejnou oblastí buněk. Funkce SUMIF() může mít ale nepovinně ještě třetí parametr. Tímto parametrem je oblast buněk, které mají být sečteny. Kontrola na splnění podmínky pak probíhá nad oblastí uvedenou v prvním parametru, vlastní sčítání pak nad oblastí uvedenou ve třetím parametru. Použití je předvedeno na Obr. 36.

Na Obr. 36 jsou dvě oblasti čísel. V první oblasti jsou kladná a záporná čísla, ve druhé oblasti (stejné velikosti a tvaru jako oblast první) jsou pak uvedené konkrétní hodnoty. Mají se sčítat ty hodnoty z druhé oblasti, kterým v první oblasti odpovídají kladná čísla. Vzájemně si odpovídající buňky v obou oblastech jsou zvýrazněny žlutě.

Obdobně jako funkci SUMIF() je možné použít také funkce:

• COUNTIF(), která určí počet hodnot odpovídajících zadané podmínce
• AVERAGEIF(), která určí hodnotu aritmetického průměru hodnot odpovídajících zadané podmínce

Kromě těchto funkcí lze použít i funkce SUMIFS(), COUNTIFS() a AVERAGEIFS(), které je možné použít v případě, že je potřeba vyhodnocovat více podmínek (Tyto funkce mají přes podobný název jiné pořadí vstupních parametrů). Tyto funkce ale nebudou v rámci tohoto textu blíže demonstrovány.

Shrnutí kapitoly

V této kapitole byly obecně popsány funkce, pomocí kterých je možné v tabulkovém procesoru jednoduše provádět i složité výpočty. Mezi hlavní poznatky patří následující informace:

• Každá funkce se skládá z názvu a parametrů. Název většinou charakterizuje výpočet, který funkce provádí, parametry představují většinou data, nad kterými je výpočet prováděn.
• Jako vstupní parametr je možné použít nejen pevně určená čísla, ale také odkazy na buňky nebo oblasti buněk.
• Některé funkce mohou mít proměnný počet parametrů.
• Jednotlivé parametry se oddělují středníkem.
• Vstupním parametrem může být i jiná funkce (bylo by možné hovořit o vnořování funkcí). Program nejprve spočítá vnitřní funkci a výsledek předá vnější funkci. Pokud se změní vstupní data pro vnitřní funkci, dojde v důsledku této změny i k přepočtu vnější funkce.
• Vestavených funkcí je v moderních tabulkových procesorech velké množství a není prakticky možné si je všechny zapamatovat. Informace o méně známých funkcích je možné nalézt v nápovědě příslušného programu. Je možné tak využít různých pomocníků a průvodců, které funkce třídí do logických skupin a umožňují v nich vyhledávat i na základě stručného popisu.
• V různých tabulkových procesorech mohou mít ekvivalentní funkce různé názvy (např. české vs. anglické názvy).
• Pro určení minimální a maximální hodnoty se v Excelu používají funkce MIN() a MAX().
• Pro výpočet součtu velkého množství hodnot se v Excelu používá funkce SUMA().
• Pro výpočet aritmetického průměru v Excelu je možné použít funkci PRŮMĚR().
• Pro výpočet směrodatných odchylek se v Excelu používají funkce SMODCH() a SMODCH.VÝBĚR().
• Užitečným typem funkcí jsou tzv. podmíněné výrazy, které umožňují provádět různé druhy výpočtu v závislosti na tom, je-li nebo není-li splněna určitá vstupní podmínka. Typickou podmíněnou funkcí je funkce KDYŽ().
• Ačkoli moderní procesory disponují velkým množstvím funkcí, může se stát, že pro některé výpočty příslušnou funkci nemají. Často je ale možné chybějící funkci nahradit kombinací jiných funkcí, např. vážený průměr lze nahradit kombinací funkcí SKALÁRNÍ.SOUČIN() a SUMA().