Pro efektivní práci s daty je možné využít tzv. tabulkových procesorů. Z nejznámějších programů tohoto typu je možné jmenovat Excel z kancelářského balíku Microsoft Office a Calc z projektu OpenOffice.org (a z něj odvozených projektů, jako je např. LibreOffice).
Již z názvu vyplývá, že tyto programy slouží k manipulaci s daty s využitím tabulek. Kromě zadávání údajů do tabulek umožňují také k definování nejrůznějších vztahů mezi těmito daty, jako jsou funkční závislosti, grafy nebo barevné vizualizace dat.
Buňky
Základem veškeré práce v tabulkových procesorech jsou tabulky. Každá tabulka se skládá z elementárních částí, tzv. buněk. Buňku si je možné představit jako políčko v nějakém formuláři, do kterého je možné zapsat nějakou hodnotu, vzorec, text apod. Na Obr. 1 ukazuje červená šipka na jednu buňku v programu Excel.
Na Obr. 1 není buňka vyznačená červenou šipkou jedinou buňkou, v jejím okolí se vyskytuje mnoho dalších buněk. Buňka vyznačená na Obr. 1 červenou šipkou má své okraje zvýrazněné tlustou černou čárou s malým čtverečkem v pravé dolní části. Toto vizuální zvýraznění informuje o tom, že se jedná o aktuálně vybranou buňku v tabulce. Pokud by uživatel programu začal psát, jím vložený text by se vložil právě do této buňky.
Změna vybrané buňky je snadno proveditelná kliknutím myši na jinou buňku nebo pomocí šipek na klávesnici.
Buňky mají pravoúhlý tvar, díky kterému je možné je snadno uspořádat do tzv. sloupců a řádků. Konkrétní sloupce se označují pomocí písmen, řádky pomocí čísel. Díky tomu je možné při práci jednoznačně adresovat konkrétní buňku. Název buňky je složen z názvu sloupce a čísla řádku, na kterém se určitá buňka nachází. Označení buňky na Obr. 1 je C3 (nachází se ve sloupci C na jeho třetím řádku).
Vzorce
Zadávání dat (např. výsledků měření) je velice snadné, stačí vybrat buňku a začít psát. Největší síla tabulkových procesorů ale spočívá v dalším zpracování zadaných dat. Nejčastěji se jedná o nejrůznější výpočty nad zadanými daty, např. základní matematické operace sčítání, odčítání, násobení nebo dělení. Od kalkulačky se tabulkový procesor liší v možnosti odděleného zadávání dat (čísel) a operací nad nimi (např. jejich součin).
Pro zadání určité matematické operace se používají tzv. vzorce. Vzorec si lze představit jako rovnici, která může obsahovat čísla, proměnné hodnoty, funkce atd. Aby tabulkový procesor poznal, že je v buňce zapsán vzorec, který musí vyhodnotit, je nutné mu poskytnout informaci o tom, že uživatel zadal vzorec a ne např. obyčejný, statický text. Proto je nutné na začátku každého vzorce uvést rovnítko (znak =).
Zadávání vzorců
Nejjednodušším vzorcem může být sečtení dvou čísel, např. 1 a 2. Vzorec se zadá tak, že uživatel napíše „=1+2“ (Obr. 2, vlevo). Dokud uživatel nestiskne klávesu Enter (nebo neopustí buňku jiným způsobem), je vzorec ve fázi zápisu a je tedy viditelný. V okamžiku, kdy uživatel stiskne klávesu Enter, potvrzuje zadaný vzorec jako hotový. V tu chvíli tabulkový procesor provede výpočet zadaného vzorce, a je-li zadán správně, zobrazí v buňce místo vzorce výsledek (Obr. 2, vpravo).
Je nutné si uvědomit, že i když v buňce C3 je zobrazeno číslo 3, obsahem dané buňky je stále zadaný vzorec. Když byl v předcházejících odstavcích vzorec připodobněn rovnici, mohlo zvídavější čtenáře napadnout, že do buňky byla zapsána pouze polovina rovnice. Tak tomu skutečně je, druhou, nezadanou část rovnice, pak představuje zobrazený výsledek.
Při opětovném vybrání buňky C3 je možné současně vidět jak výsledek („levou část“ rovnice), tak zadaný vzorec („pravou část“ rovnice), jak znázorňuje Obr. 3.
Vzorec na Obr. 3 je zobrazen v oblasti zvané řádek vzorců. Pokud je nutné vzorec upravit, je možné provést tuto úpravu právě v řádku vzorců. Alternativní možností je vybrat buňku, jejíž vzorec je určen k upravení, a stisknout funkční klávesu F2. Ta způsobí přepnutí zobrazení buňky z výsledku na vzorec (aplikace se dostane do stavu z Obr. 2 vlevo).
Vzorce s odkazy
V předchozí kapitole byl demonstrován základní způsob zadávání vzorců. Jednoduché operace s pevně zadanými čísly, na kterých bylo zadávání vzorců předvedeno, umožňuje i ta nejjednodušší kalkulačka. Je zřejmé, že takovéto použití by tabulkový procesor značně degradovalo, nehledě na to, že podobné triviální operace se do kalkulačky zadávají snadněji a efektivněji.
Již bylo řečeno, že síla tabulkového procesoru spočívá v možnosti oddělit zadání vstupních dat (v předchozím případu se jednalo o čísla 1 a 2) a matematické operace s těmito čísly (v předchozím případě se jednalo o součet).
Toto oddělení je realizováno tak, že:
- Do dvou libovolných buněk jsou zadána vstupní data (sčítaná čísla).
- Do třetí buňky se zadá stejný vzorec, ale s tím rozdílem, že místo čísel se použijí názvy buněk, které obsahují sčítaná čísla.
Jedná se o podobnou situaci, jako kdyby se nejprve stanovilo, že x = 1 a y = 2 a poté napsalo, že z = x + y. Pokud by podobnou rovnici řešil člověk, přepsal by ji nejprve do tvaru z = 1 + 2 (nahradil by písmena jejich hodnotami) a teprve poté vypočítal výsledek. Obdobným způsobem pracuje i tabulkový procesor. Popsaný příklad je ilustrován na Obr. 4.
Názvy buněk není nutné do vzorce zadávat ručně (to s sebou přináší i riziko chyby plynoucí z chybného zadání), ale je možné využít kliknutí myši nebo šipek klávesnice. Příklad z Obr. 4 by se v bodu 3 realizoval takto:
- Uživatel by v buňce B6 napsal rovnítko
- Kliknul by do buňky B3 (program by doplnil do vytvářeného vzorce příslušný název buňky)
- Napsal by + (znaménko pro sčítání)
- Kliknul by do buňky B4 (opět by se do vytvářeného vzorce název zvolené buňky doplnil automaticky)
- Stisknul by klávesu Enter
Výhoda oddělení dat od způsobu jejich zpracování nemusí být na první pohled zřejmá. Spočívá v tom, že tabulkový procesor automaticky přepočítává všechny vzorce v okamžiku, kdy se vstupní data změní. Pokud by došlo ke změně hodnoty v buňce B3 z jedničky na dvojku, automaticky by došlo k přepočítání hodnoty v buňce B6 na 4, jak ilustruje Obr. 5.
Kopírování vzorce do více buněk, relativní odkazy
V předcházejícím příkladu tabulkový procesor sečetl čísla z buněk B3 a B4. Přestože uživatel uvedl konkrétní názvy buněk (a program ty samé konkrétní názvy buněk zobrazuje), nejsou ve vzorci názvy buněk uloženy napevno. Program si ve skutečnosti pamatuje jejich relativní pozici vůči vzorci. Při vyhodnocování vzorce tedy ví, že první hodnotu najde ve stejném sloupci, v jakém je zadán vzorec, o tři buňky výše, a druhá hodnota že je umístěna taktéž ve stejném sloupci o dvě buňky výše.
Díky tomu je možné vzorec nakopírovat (Ctrl+C a Ctrl+V) do jiné buňky a takto vzniklá kopie bude opět sčítat dvě hodnoty o tři, resp. dvě místa výše. Tato vlastnost tabulkových procesorů je znázorněna na Obr. 6.
Kopírování vzorce metodou kopírovat-vložit je relativně pohodlné, ale při větším objemu dat pracné. Většina moderních tabulkových procesorů umožňuje velmi efektivní rozšiřování vzorců do okolních buněk. Základním předpokladem je, že kopie mají vzniknout v sousedních buňkách (vodorovných či svislých). Může to působit omezujícím dojmem, ale pravdou je, že se jedná o nejčastější případ.
Rozšíření vzorce do okolních buněk se provádí táhnutím za malý čtvereček (tzv. úchyt), který je v pravém dolním rohu (Obr. 7) buňky obsahující kopírovaný vzorec.
Jednu z možných výchozích situací zachycuje Obr. 8. Rozšíření vzorce se provede kliknutím na úchyt a jeho přetažením ve směru červené šipky.
Oblast, do které bude vzorec rozšířen, je během táhnutí znázorňována pomocí tečkovaného okraje (zobrazeno na Obr. 9).
Po puštění tlačítka myši se vzorec rozkopíruje do zvolené oblasti (Obr. 10, bod 1) a díky relativnímu odkazu se v každém sloupci aplikuje na správné hodnoty (Obr. 10, bod 2).
Obdobným způsobem by se postupovalo i v případě, že by bylo zapotřebí vzorec rozšířit svislým způsobem.
Absolutní odkazy
Někdy může být žádoucí, aby i v rozkopírovaných vzorcích zůstaly některé odkazy stejné jako v prvním vytvořeném vzorci. Takovým případem může být například výpočet procentuální odchylky od určité hodnoty.
Procentuální odchylku lze vyjádřit jako poměr mezi rozdílem skutečné a teoretické (např. předepsané) hodnoty a teoretickou hodnotou. Formálním popisem vztahu by mohl být vzorec:
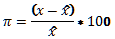
,kde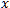 
je naměřená hodnota a 
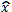je hodnota teoretická.
Obr. 11 ilustruje výchozí situaci, kdy je v buňce C2 zadaná předepsaná hmotnost určitého výrobku, a na řádcích 6-15 ve sloupci B jsou naměřené skutečné hmotnosti deseti vybraných výrobků. Cílem vyhodnocení je určit, o kolik procent se naměřená hmotnost liší od deklarované.
Vzorec uvedený vedle první naměřené hmotnosti (tzn. v buňce C6) se odkazuje do buňky o jedno místo od vzorce vlevo, kde je uvedená naměřená hmotnost, a do buňky o jedno místo od vzorce vlevo a čtyři místa nahoru, kde je uvedená předepsaná hmotnost. Při rozkopírování tohoto vzorce do ostatních řádků se zobrazí výsledky, které již na první pohled neodpovídají očekávaným hodnotám (viz Obr. 12).
Důvodem je, že kromě odkazů na naměřené hodnoty (kde je změna odkazu potřebná) došlo i ke změně odkazu na buňku obsahující předepsanou hodnotu. To je patrné z Obr. 12, kde např. v buňce C7 tabulkový procesor hlásí chybu „Dělení nulou“. Z řádku vzorců je příčina zřejmá, odkaz do buňky B2 se změnil na odkaz do buňky B3, která neobsahuje žádnou hodnotu. Prázdná buňka je interpretována jako buňka obsahující nulu, kterou dělit nelze.
Již na tomto příkladu je patrné, že relativní odkazy v tomto případě komplikují správný výpočet. Daleko vhodnější by bylo, kdyby v případě buňky obsahující předepsanou hmotnost nedošlo při rozkopírování vzorce k úpravě odkazu na tuto buňku (tedy aby i kopie původního vzorce stále odkazovaly do buňky B2). Naopak v případě naměřených hodnot je zapotřebí, aby se na každém řádku odkazovaly do jiné buňky.
Řešením tohoto problému jsou tzv. absolutní odkazy. Absolutní odkaz je takový odkaz, který i při kopírování vzorce odkazuje stále na stejnou buňku. Zapisuje se obdobným způsobem jako relativní odkaz s tím rozdílem, že před název sloupce a číslo řádku se uvede znak $. Odkaz na buňku B2 by tedy byl zapsán jako $B$2 (viz Obr. 13, bod 1).
Znak $ je možné uvést také pouze před znak sloupce nebo pouze před číslo řádku. V takovém případě je vytvořený odkaz absolutní pouze z hlediska sloupce (resp. řádku) a při kopírování vzorce se mění pouze ta část odkazu, která není znakem $ označená
Z bodu 2 na Obr. 13 je patrné, že při rozkopírování vzorce využívajícího absolutní odkazy jsou hodnoty procentuálních odchylek vypočítány správně. Při bližším prozkoumání vzorce v buňce B7 je také patrné, že první odkaz ve vzorci se změnil z B6 a B7 (jednalo se o relativní odkaz, bez znaku $), zatímco druhý a třetí odkaz vzorce (do buňky s předepsanou hodnotou) zůstal zachován, protože byl zadán jako odkaz absolutní.
Zadávání absolutních odkazů
Znak $ se na české klávesnici standardně nevyskytuje, proto by zadávání absolutních odkazů s přímým zápisem tohoto znaku mohlo být příliš komplikované (bylo by nutné např. přepínat klávesnici z české na anglickou a zpět).
Během editace je ale možné (i opakovaně) využívat funkční klávesu F4, která znak $ doplní do odkazu, na kterém se aktuálně nachází klávesnicový kurzor („blikající svislá čárka“). Způsob využití této funkční klávesy je znázorněn na Obr. 14.
Blok buněk
Někdy může být výhodné označit více buněk současně. Většina tabulkových procesorů umožňuje označovat pravoúhlé oblasti buněk. Označení je možné provést např. tak, že uživatel myší klikne do buňky, která má být některým z rohů oblasti, a táhnutím myši označuje další buňky. Kliknutím do jakékoli jiné buňky je označení oblasti zrušeno.
Je-li zapotřebí tuto oblast adresovat, použije se odkaz na buňku levého horního rohu a pravého dolního rohu oblasti a odkazy se oddělí dvojtečkou. Oblast označená na Obr. 15 by se formálně popsala C3:D6.
I s oblastmi buněk je možné provádět jednoduché výpočetní operace, velmi elegantně se s těmito oblastmi pracuje jako s maticemi. Konkrétní využití oblastí buněk bude demonstrováno v pozdějších kapitolách, především v kapitole Základní funkce.
Shrnutí kapitoly
V této kapitole byl přednesen stručný úvod do práce s tabulkovým procesorem. Mezi hlavní poznatky patří následující informace:
- Tabulkový procesor dělí tabulky do tzv. buněk. Každou buňku je možné jednoznačně adresovat pomocí označení příslušného sloupce (písmeno) a řádku (číslo).
- Nad hodnotami v různých buňkách je možné provádět matematické operace a výsledky těchto operací zobrazovat v jiných buňkách. K tomu slouží tzv. vzorce, které kromě matematických operátorů obsahují také odkazy na jiné buňky, ze kterých je během výpočtu přenesena jejich hodnota. Tabulkový procesor výsledky vzorců přepočítá při každé změně dat.
- Odkazy na jiné buňky jsou nejčastěji definované relativně vůči buňce se vzorcem (jako počet buněk ve vodorovném a svislém směru, který je potřeba projít z buňky obsahující vzorec, aby byla nalezena buňka s příslušnou hodnotou). Díky tomu je možné s jednou zadaným vzorcem opakovaně provádět určitý výpočet nad různými buňkami.
- Za určitých podmínek může být výhodné definovat odkaz jako absolutní. V případě rozkopírování vzorce obsahujícího absolutní odkazy nedojde v jeho kopiích ke změně těchto odkazů (i kopie vzorce se budou odkazovat na stále stejnou buňku).
- Buňky mohou tvořit větší seskupení (tzv. oblasti) a některé operace je možné provádět nad všemi buňkami v dané oblasti.